Оценка стоимости финансовых инструментов, производных от процентной ставки

Для оценки стоимости финансовых инструментов, производных от процентных ставок, используются модели временной структуры процентных ставок с непрерывным временем.

Временная структура процентных ставок определяется внутренними доходностями облигаций с нулевыми купонами при различных сроках до погашения. Таким образом, процентная ставка 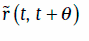при непрерывном начислении в момент времени t по инвестициям на θ лет удовлетворяет равенству:

Следовательно, зная траекторию краткосрочной процентной ставки на некотором временном промежутке, можно определить и временную структуру процентных ставок на этом промежутке.

Во многих моделях временной структуры процентных ставок эволюция краткосрочной процентной ставки задается с помощью стохастических дифференциальных уравнений.

Предположим, что краткосрочная процентная ставка rт определяется случайным процессом Ито, т. е.

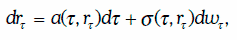
и удовлетворяет начальному условию rt = r0.

Рассмотрим финансовый инструмент, производный от процентной ставки, по которому не выплачиваются доходы. Стоимость такого инструмента у в момент ? определяется двумя факторами: краткосрочной процентной ставкой rτ (далее – r) и самим моментом τ, т. е.

При отсутствии арбитражных возможностей стоимость любого финансового инструмента, по которому не выплачиваются доходы, должна удовлетворять следующему дифференциальному уравнению в частных производных (1):

Таким образом, чтобы найти стоимость финансового инструмента, производного от процентной ставки, необходимо задать коэффициенты α(τ, r) и σ(τ, r) стохастического дифференциального уравнения, которому удовлетворяет краткосрочная процентная ставка, определить рыночную цену риска λ(τ, r) и найти решение дифференциального уравнения (1) при соответствующих граничных и начальных условиях.

В мире, нейтральном к риску, рыночную цену риска λ(τ, r) естественно считать равной нулю.

Если выполняются условия:

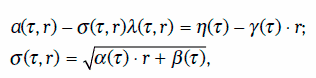
то стоимость облигации с нулевым купоном РТ(τ) номиналом 1 долл. и датой погашения Т можно найти по формуле: